Writing a Chess Engine
The goal was to write a programm that can beat me consistently in a game of chess (not that hard). Code available at my github.
Programming Chess
Before even considering the search, at its core a chess engine has to be able to simulate a chess game. It is critical to be able to generate all possible moves for a given position very fast.
Board Representation
The best way to represent a chess board is to use an unsigned 64 bit integer for each piece and each player. Additionally, en-passant and castling rules have to be stored.

This way we can work with fast bitwise operations. For exampe knigths & blacks gives an integer representening all positions occupied by black knights.
Move Generation
For every piece and every board tile all possible moves if the board was empty are precomputed and stored. In addition, for every pair of board tiles the first tile emits a ray and the second tile casts a shadow on the board which is stored. The tiles between a pair of tiles is also precomputed.
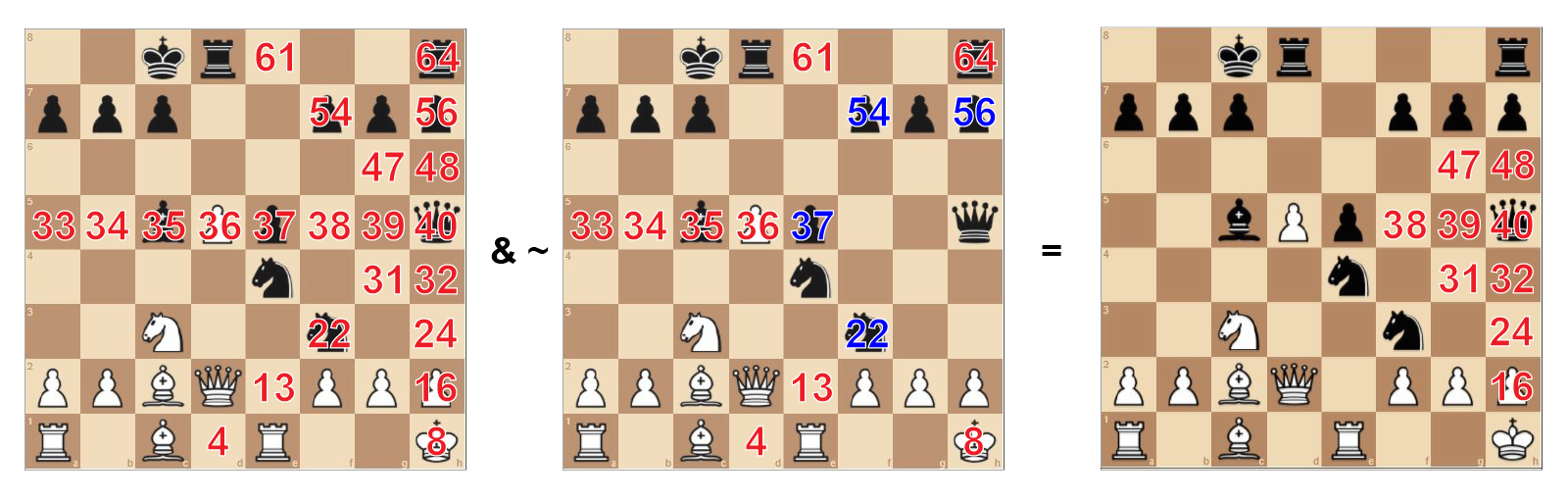
First, all pinned pieces are computed at once. These are pieces that cannot be move because the king would be in check.
Then, for each unpinned piece, for example the queen, we take all possible moves if the board was empty (left picture) and substract all shadows of hit pieces (red in mid picture) and own pieces (blue in mid picture). As a result we get all fields were the queen can move to (right picture).
Pawn and king moves take extra care (capture is different from pushing, en passant, castling, cannot move into check).
If the king is in check, the player is only allowed to make moves after which the king is not in check anymore. If this is not possible it is checkmate. To accommodate this, I simply try the move, check if the king is in check, and then undo the move (this can be made more efficient but it happens rarely enough).
Performance
With my implementation I am able to generate up to 100 million board positions per second.
Evaluation
The evaluation function is arguably the most important aspect of a chess engine. If I know which position is winning and which position is loosing I would only need to investigate the immediate moves and all further search would be redundant. Such function can be attempted to learn with machine learning, can be handcrafted based on existing chess theory, or can be a combination of both.
I did not include any learning yet and crafted an evaluation function from my knowledge. It includes a basic piece count (pawn=1, bishop=knight=3, rook=5, queen=9), penalises bad pawn structure (isolated, doubled pawns), rewards passed pawns and the occupation of the center squares and encourages knight and bishop development. King safety is estimated by rewarding a king at the sides of the board behind pawns. In the endgame the advancement of pawns is rewarded and the king safety not that much enforced anymore. If the opponent does only have pawns, the players king is encourage to force the other king into corners to find checkmates in winning positions.
As at is now, the evaluation function seems to work fine but results also in unwanted behavior which is discussed further down.
Search
Minimax
The Minimax-Algorithm is a basic search algorithm for zero-sum two person games with perfect information like chess. It assumes that one party wants to maximise the score while the other wants to minimise the score. In chess usually white is the one to maximise the score. At it's core, the Minimax-Algorithm wants to find the move that maximises the minimal obtainable board value after the move for white and minimise the maximal obtainable board value after the move for black. This logic can be applied recursively. For any evaluation function determines the optimal move if the search reaches all terminal nodes which is impossible in chess. Thus, the algorithm is only executed up to a certain depth.
function minimax(board, white, depth)
moves = get_moves(board, white)
if length(moves) == 0 || depth == 0
return eval(board)
end
if white
value = MIN_VALUE
for move in moves
make_move(board, move)
value = max(value, minimax(board, !white, depth-1))
undo_move(board, move)
end
else
value = MAX_VALUE
for move in moves
make_move(board, move)
value = min(value, minimax(board, !white, depth-1))
undo_move(board, move)
end
end
return value
end
AlphaBeta
The AlphaBeta-Algorithm is an improvement over the Minimax-Algorithm.
It employs a basic pruning strategy.
It adds two variables to the search which represent the worst case scenario for each player.
By convention, alpha is the minimum value that white can achieve, while beta is the maximum value that black can achieve.
If we are at a node for white and we find a move with value that exceeds beta we stop the search at this node (beta-cutoff) because black already knows a line were the worst case would result in beta.
So black would prevent the current line from happening.
An equivalent statemant can be made if black is to move where we speak of an alpha-cutoff.
Quiescence Search
If we simply stop at a certain search depth and use the current board value we may overlook that our queen could be captured next move which would drastically change the value (horizon effect). To avoid this I perform at each leaf all possible capture moves in the best move order (AlphaBeta). When there are no more captures possible the board is considered quiet. This could be extended to look for checkmates as well.
function alphabeta(board, white, depth, alpha, beta)
moves = get_moves(board, white)
if length(moves) == 0 || depth == 0
return quiesce(board, white, alpha, beta)
end
if white
value = MIN_VALUE
for move in moves
make_move(board, move)
value=max(value,alphabeta(board,!white,depth-1,alpha,beta))
undo_move(board, move)
alpha = max(alpha, value)
if alpha >= beta break
end
else
value = MAX_VALUE
for move in moves
make_move(board, move)
value=min(value,alphabeta(board,!white,depth-1,alpha,beta))
undo_move(board, move)
beta = min(beta, value)
if alpha <= beta break
end
end
return value
end
MTD(f)
A null window search is a AlphaBeta call with minimal window size alpha = v-1, beta = v for some value v.
This leads to many cutoffs and is thus a more narrow search.
If we guess the value to be v and the search returns a higher value then we can be sure that v is a lower bound. Conversely, if it returns a lower value we have an upper bound.
The MTD(f)-Algorithm uses this fact and performs many null window searches until lower and upper bound converge. If we guess the value correctly, only two null window searches are necessary for termination. This algorithm is fast if we memoize and reuse the computed values from previous searches.
function MTDF(board, white, depth, guess)
value = guess
upper = MAX_VALUE
lower = MIN_VALUE
while lower < upper
beta = max(value, lower + 1)
value = AlphaBeta(board, white, depth, beta-1, beta)
if value < beta
upper = value
else
lower = value
end
end
return value
end
Iterative Deepening
As the name suggests it can be beneficial to iteratively increase the search depth. Shallower searches are faster and we get a better and better value estimate that can be used as starting point for the next depth. I sped up the search by reusing the search tree from shallower depths.
function IterativeMTDF(board, white, min_depth, max_depth)
value = 0
for depth in min_depth:max_depth
value = MTDF(board, white, depth, value)
end
return value
end
Performance Comparison
The following position was searched up to depth 6 (plus quiescence search). The table shows the number of explored nodes and spent time for different algorithms. For comparison the required time to generate all reachable positions is given.
| Number of Nodes | Time | |
|---|---|---|
| Move Generation | 873 377 600 | 7.694s |
| AlphaBeta | 832 634 | 1.092s |
| MTD(f) | 658 447 | 0.851s |
| Iterative MTD(f) | 518 774 | 0.626s |
Opening
A human chess player has to study a lot of theory to survive the opening on a competitive level. We can collect all available theory in a table from which every position can be looked up in an instant. I only included some opening theory of the queen's gambit.
Endgame
When the number of pieces on the board is small there is a chance that it is a theoretical win, draw or loss. However, even for simple configurations, like king + queen vs king, it is possible that it takes up to 28 moves to checkmate. My engine is too slow to find such a mate and here it is beneficial to employ endgame tablebases, essentially precomputed checkmates.
For a three piece tablebase this is not too difficult and works like this: Generate all positions with two kings and rook, or queen. Now filter for all positions were black is mated. Then go one ply back. Cool, we have found all mates in 1. Now, search for all positions were regardless of blacks move white can deliver mate. I call these desperate positions in 1. Then continue for mates in 2, desperate positions in 2, etc.
The known mates and desperate positions are stored in a dictionary with the number of required moves. This way we can later find the quickest mate. If a position with three pieces is not in the table it is a draw.
positions = generate_all_3_piece_boards()
new_desperate_positions = find_checkmates(positions)
all_desperate_positions = new_desperate_positions
all_mates = []
i = 0
while length(new_desperate_positions) > 0
i += 1
# find all mate in i
new_mates = find_mates_in_next_move(new_desperate_positions)
append(all_mates, new_mates)
# find all positions where each moves leads to known mate
dps = find_desperate_positions(all_mates)
# filter for new desperate positions
new_desperate_positions = setdiff(dps, all_desperate_positions)
append(all_desperate_positions, new_desperate_positions)
end
Now our engine has flawless endgame technique (when three pieces are on the board).
Best Games
Highest win against chess.com engine level 20 (2400).
Brilliant 44th move leads to winning queen with tactics.
Simplification to winning endgame against chess.com engine level 12(1600).
Nice knight, bishop, rook checkmate against chess.com engine level 14 (1800).
Endgame fight against chess.com engine level 14 (1800).
Doesn't even take the queen.
The final standings after playing 6 games against chess.com engines of several levels can be seen in following table.
| chess.com engine | white | black | total |
|---|---|---|---|
| 12 (1600) | 3.0 | 3.0 | 6.0 |
| 13 (1700) | 3.0 | 3.0 | 6.0 |
| 14 (1800) | 1.5 | 3.0 | 4.5 |
| 15 (1900) | 1.0 | 2.5 | 3.5 |
| 16 (2000) | 2.0 | 2.0 | 4.0 |
| 17 (2100) | 0.0 | 0.5 | 0.5 |
| 18 (2200) | 1.5 | 0.5 | 2.0 |
| 19 (2300) | 0.0 | 0.0 | 0.0 |
| 20 (2400) | 0.5 | 1.0 | 1.5 |
| 21 (2500) | 0.0 | 0.0 | 0.0 |
So I would estimate my engine's strenght at 2000-2100 (against bots).
Possible Improvements
Fixing Weaknesses With Better Board Evaluation
If the queen is on its original position the engine will sometimes try to "castle manually" out in the open. In the following position the white's move was Kd2 which is immediately punished by stronger opponents.
For the following position my engine suggests Rxe5 misjudgeing a simplification to pawn endgame.
Including Threefold Repetition Detection
In some positions the engine blunderes a threefold repetion from a winning position as it does not know that the rule exists - yet.
Improving Quiescence Search
Now most of the search time is spent in the quiescence search. This should be improved to search deeper.
Adjusting Search Depth Dynamically
If the opponent delivers check or threatens the king an extended search should be performed. As of now the engine misses longer mateing patterns.
Extending Endgame Tablebase
Generate 5-men and/or pawn endgame tablebases.
Extending Opening Book
Include more theory so that engine does not have to come up with opening theory on the fly (and castles manually).
More pruning
We have to go deeper! Now the usual search depth (without quiesce) is at 7-8 plys. Too few. Null move pruning, razoring, better move order could improve that.
Principal Variation Search Instead of AlphaBeta
MTD(f) may be faster with PVS. A good transposition table (store only frequent positions) could be also beneficial.
Use Opponents Time
Anticipate opponents move and search on their clock.
Keep Search Tree
Do not throw away the search tree after making a move. Only prune the branches which were not played.
Multi Threading
A multi threading would speed up the search significantly. It is unlikely that I am able to do that, though.
Did I Achieve My Goal?
Yes, the engine beats me without a drop of sweat :).
Try it your self! Instructions here. JULIA required.