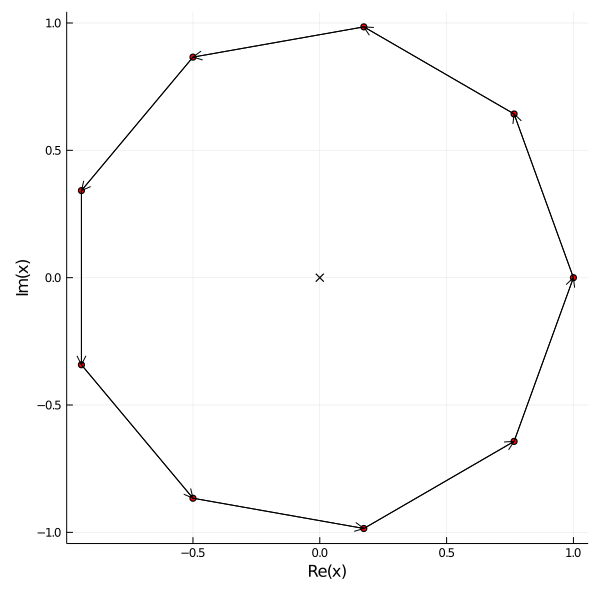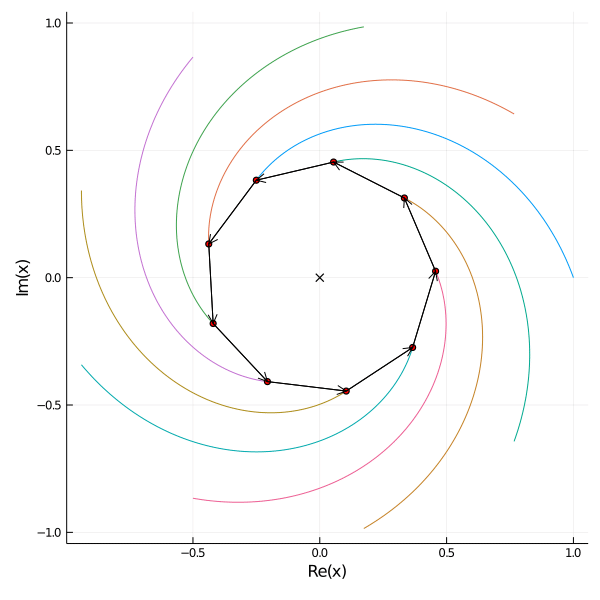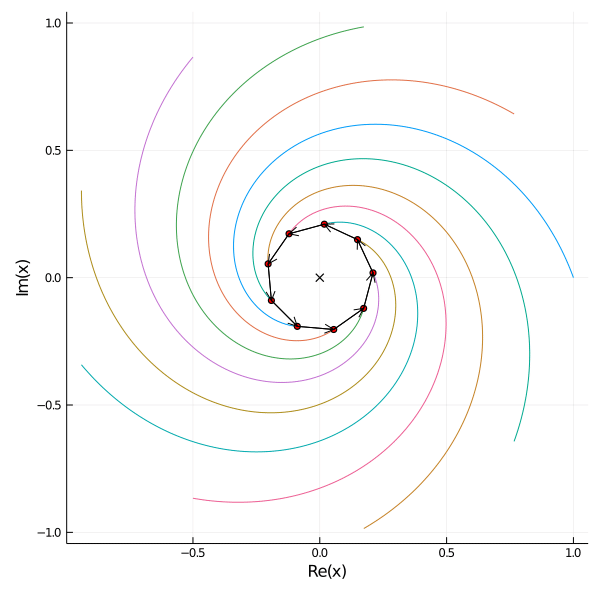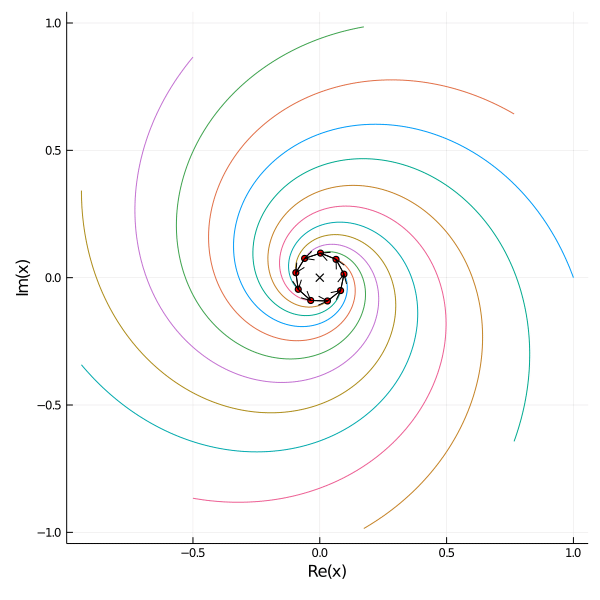
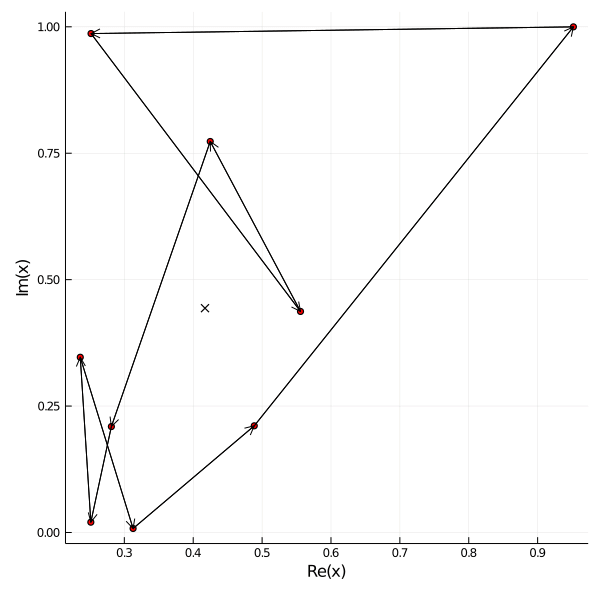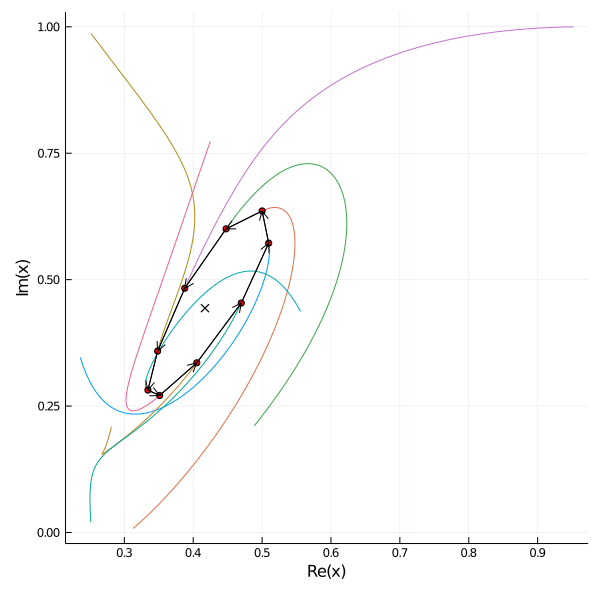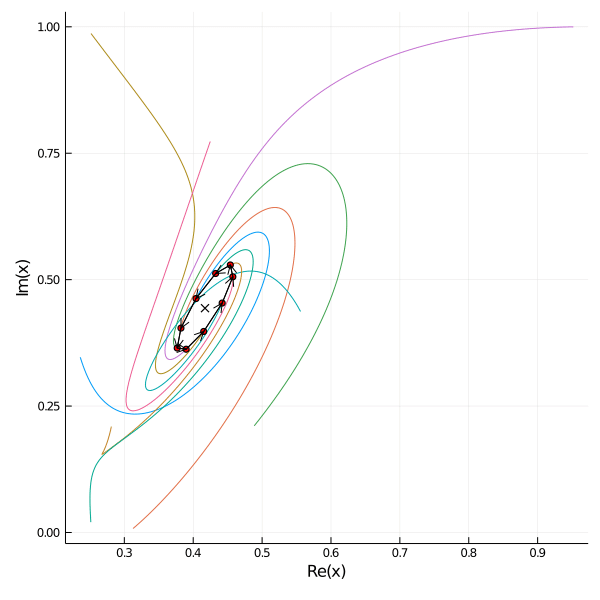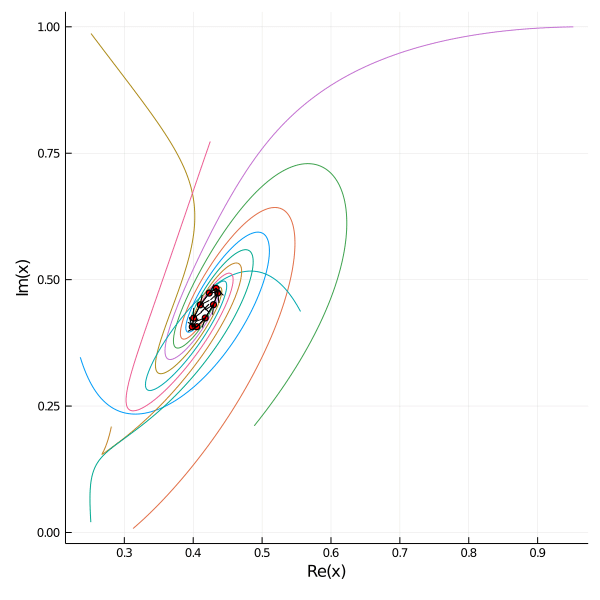
Consider following scenario: \(n\) mice \(x_1, \dots, x_n \in \mathbb{C}\) are spread on a plane. Each mouse \(x_j\) follows the next mouse \(x_{j+1}\) and the last mouse follows the first one again. The velocity equals the distance between the mice. We can write this scenario in terms of a system of linear equations: \begin{align*} \dot{x}_j &= x_{j+1} - x_j, \quad j \in 1, \dots n-1, \\ \dot{x}_n &= x_1 - x_n. \end{align*}

This system can be considered to be of form \[\dot{\mathbf{x}} = A\mathbf{x} \in \mathbb{C}^n. \] We can find the solutions of the differential equations by finding eigenvalues and eigenvectors \begin{align*} \lambda x_j &= x_{j+1} - x_j, \quad j \in 1, \dots n-1, \\ \lambda x_n &= x_1 - x_n. \end{align*} It is easy to see that \[x_n = (\lambda + 1)x_{n-1} = (\lambda + 1)^2 x_{n-2} = \dots = (\lambda + 1)^{n-1} x_1.\] Since \(x_1 = (\lambda + 1) x_n\) we have \[x_1 = (\lambda + 1)^n x_1.\] Solving for \(\lambda\) yields \[\lambda = \sqrt[n]{1} - 1 = \exp\left(\frac{2\pi i k}{n}\right) - 1 = \zeta_n^k - 1 \quad j \in 1, \dots, n.\] By the previous recursion the corresponding eigenvalues are also readily found \begin{align*} \text{for} \quad \lambda = \zeta_n^k - 1 \quad v = (1, \zeta_n^{k}, \zeta_n^{2k}, \dots \zeta_n^{(n-1)k})^\top. \end{align*}

If the mice are initially positioned at the roots of 1 the solutions are given by \begin{align*} x_j(t) = \zeta_n^{j-1} \exp((\zeta_n - 1)t). \end{align*}

For arbitrary initial positions \(\mathbf{x}_0 \in \mathbb{C}^n\) let \(V\) denote the \(n \times n\) matrix of eigenvectors. We solve for \[V\mathbf{c} = \mathbf{x}_0.\] Then the solutions are \begin{align*} x_j(t) = \sum_{k=1}^n c_k \zeta_n^{k(j-1)} \exp((\zeta_n^k - 1)t). \end{align*} As \(|\zeta_n^k - 1| < 1\) for all \(k\) and \(|(\zeta_n^n - 1)| = 0\) the functions converge to \(c_n\) as \(t \to \infty\) which is equal to the midpoint of the starting postions \(c_n = \frac{1}{n} ||\mathbf{x}_0||_1\).

Here are examples of 9 mice placed on the roots of 1 on the left and placed randomly on the right.