The following is based on this lecture from Grant Sanderson.
Seam Carving is a technique used to reduce image size. Unlike simply scaling the image, this method tries to preserve the aspect ratios of the main objects of the image.
This task can be achieved by detecting the edges of the objects and then take a path from top to bottom (or left to right) which crosses the least edges - the S E A M.
How to detect edges?
Edge detection can be done by convolving the image with an appropriate kernel.
The Sobel filter is a good choice:
\[
\begin{align*}
\begin{bmatrix}
0.125 & 0 & 0.125 \\
0.25 & 0 & 0.25 \\
0.125 & 0 & 0.125
\end{bmatrix},
\quad
\begin{bmatrix}
0.125 & 0.25 & 0.125 \\
0 & 0 & 0\\
0.125 & 0.25 & 0.125
\end{bmatrix},
\end{align*}
\]
for vertical and horizontal edges respectively.
These kernels are applied separately to the brightness values of the image,
\[\texttt{Brightness}(r,g,b) = 0.3 * r + 0.59 * g + 0.11 * b,\]
and then the Euclidean norm is computed from both components.
This achieves images similiar to this:
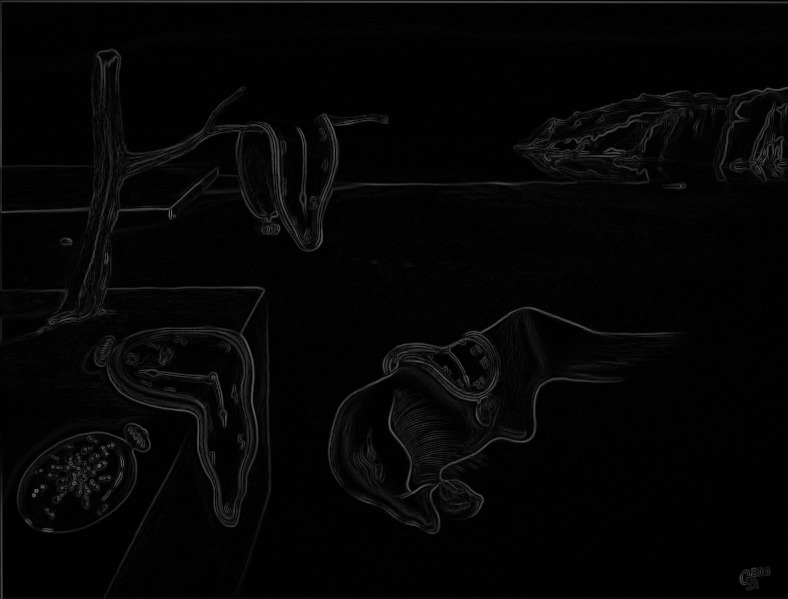
How to find the seam?
Imagine a path from top to bottom. We restrict the paths to only go down or down left or down right per row. The edgeness of this path is just the sum of all edgeness values of its pixels. We want to find the path with minimum edgeness. We have to work from bottom to top. The edgeness of the last row remains the same. Then we move one row up and assign each pixel its edgeness value from the convolution plus the minimum value of the possible next pixels of the row below. We also keep track which of the three pixels it was to retrive the path once we are finished. If we completed the last (first) row we choose the pixel with the least edgeness value. We then follow the directions we kept track of and store all traversed pixels in a list. This is then the desired path - the seam - which will be removed from the image.
Final result
